Chapter 22: Dummy Dependent Variable Models
In earlier chapters, we have created and interpreted dummy independent variables in regressions. We have seen how 0/1 variables such as Female (1 if female, 0 if male) can be used to test for wage discrimination. These variables have either/or values with nothing in between. Up to this point, however, the dependent variable Y has always been essentially a continuous variable. That is, in all the regressions we have seen thus far, from our first regression using SAT scores to the many earnings function regressions, the Y variable has always taken on many possible values.
This chapter discusses models in which the dependent variable (i.e., the variable on the left-hand side of the regression equation, which is the variable being predicted) is a dummy or dichotomous variable. This kind of model is often called a dummy dependent variable (DDV), binary response, dichotomous choice, or qualitative response model.
Dummy dependent variable models are difficult to handle with our usual regression techniques and require some rather sophisticated econometrics. In keeping with our teaching philosophy, we present the material with a heavy emphasis on intuition and graphical analysis. In addition, we focus on the box model and the source of the error term. Finally, we continue to rely on Monte Carlo simulation in explaining the role of chance. Although the material remains difficult, we believe our approach greatly increases understanding.
What Exactly Is a Dummy Dependent Variable Model?
That question is easy to answer. In a dummy dependent variable model, the dependent variable (also known as the response, left-hand side, or Y variable) is qualitative, not quantitative.
Yearly Income is a quantitative variable; it might range from zero dollars per year to millions of dollars per year. Similarly, the Unemployment Rate is a quantitative variable; it is defined as the number of people unemployed divided by the number of people in the labor force in a given location (county, state, or nation). This fraction is expressed as a percentage (e.g., 4.3 or 6.7 percent). A scatter diagram of unemployment rate and income is a cloud of points with each point representing a combination of the two variables.
On the other hand, whether you choose to emigrate is a qualitative variable; it is 0 (do not emigrate) or 1 (do emigrate). A scatter diagram of Emigrate and the county Unemployment Rate would not be a cloud. It would be simply two strips: one horizontal strip for various county unemployment rates for individuals who did not emigrate and another horizontal strip for individuals who did emigrate.
The political party to which you belong is a qualitative variable; it might be 0 if Democrat, 1 if Republican, 2 if Libertarian, 3 if Green Party, 4 if any other party, and 5 if independent. The numbers are arbitrary. The average and SD of the 0, 1, 2, 3, 4, and 5 are meaningless. A scatter diagram of Political Party and Yearly Income would have a horizontal strip for each value of political party.
When the qualitative dependent variable has exactly two values (like Emigrate), we often speak of binary choice models. In this case, the dependent variable can be conveniently represented by a dummy variable that takes on the value 0 or 1. If the qualitative dependent variable can take on more than two values (such as Political Party), the model is said to be multiresponse or multinomial or polychotomous. Qualitative dependent variable models with more than two values are more difficult to understand and estimate. They are beyond the scope of this book.
More Examples of Dummy Dependent Variables
Figure 22.1.1 gives more examples of applications of dummy dependent variables in economics. Notice that many variables are dummy variables at the individual level (like Emigrate or Unemployed), although their aggregated counterparts are continuous variables (like emigration rate or unemployment rate).
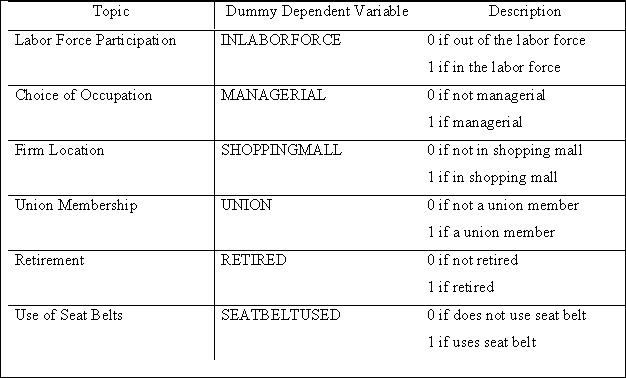
Figure 22.1.1. Applications of Dummy Variables in Economics.
The careful student might point out that some variables commonly considered to be continuous, like income, are not truly continuous because fractions of pennies are not possible. Although technically correct, this criticism could be leveled at any observed variable and for practical purposes is generally ignored. There are some examples, however, like educational attainment (in years of schooling), in which determining whether the variable is continuous or qualitative is not so clear.
The definition of a dummy dependent variable model is quite simple: If the dependent, response, left-hand side, or Y variable is a dummy variable, you have a dummy dependent variable model. The reason dummy dependent variable models are important is that they are everywhere. Many individual decisions of how much to do something require a prior decision to do or not do at all. Although dummy dependent variable models are difficult to understand and estimate, they are worth the effort needed to grasp them.
Organization
The next two sections provide intuition for the data generating process underlying the dummy dependent variable model. We emphasize the fundamental idea that a chance draw is compared with a threshold level, and this determines the observed 0 or 1 value of the dummy dependent variable. Section 22.4 continues working on the data generating process by drawing the box model that generates the observed values of 0 or 1. In Section 22.5, we introduce the linear probability model (LPM), which simply fits a line to the observed scatter plot of 0’s and 1’s. The LPM is easy to work with, but its substantial defects lead us to look for better methods. Section 22.6 uses nonlinear least squares (NLLS) to fit an S-shaped curve to the data and improve on the LPM. Nonlinear least squares is better than LPM but more difficult to interpret, and so we devote the next section to interpreting the results from the NLLS regression. We conclude the chapter with a real-world example of a dummy dependent variable that examines the issue of mortgage discrimination.
Excel Workbooks
CAMPCONT.xls
LPMMonteCarlo.xls
MortDisc.xls
MortDiscMCSim.xls
NLLSFit.xls
NLLSMCSim.xls
Raid.xls