Chapter 17: Joint Hypothesis Testing
Chapter 16 shows how to test a hypothesis about a single slope parameter in a regression equation. This chapter explains how to test hypotheses about more than one of the parameters in a multiple regression model. Simultaneous multiple parameter hypothesis testing generally requires constructing a test statistic that measures the difference in fit between two versions of the same model.
An Example of a Test Involving More than One Parameter
One of the central tasks in economics is explaining savings behavior. National savings rates vary considerably across countries, and the United States has been at the low end in recent decades. Most studies of savings behavior by economists look at strictly economic determinants of savings. Differences in national savings rates, however, seem to reflect more than just differences in the economic environment. In a study of individual savings behavior, Carroll et al. (1999) examined the hypothesis that cultural factors play a role. Specifically, they asked the question, Does national origin help to explain differences in savings rate across a group of immigrants to the United States? Using 1980 and 1990 U.S. Census data with data on immigrants from 16 countries and on native-born Americans, Carroll et al. estimated a model similar to the following:(1)
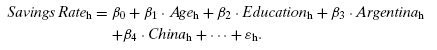
For reasons that will become obvious, we call this the unrestricted model. The dependent variable is the household savings rate. Age and education measure, respectively, the age and education of the household head (both in years). The error term reflects omitted variables that affect savings rates as well as the influence of luck. The subscript h indexes households. A series of 16 dummy variables indicate the national origin of the immigrants; for example, Chinah = 1 if both husband and wife in household h were Chinese immigrants.(2) Suppose that the value for the coefficient multiplying China is 0.12. This would indicate that, with other factors controlled, immigrants of Chinese origin have a savings rate 12 percentage points higher than the base case (which in this regression consists of people who were born in the United States).
If there are no cultural effects on savings, then all the coefficients multiplying the dummy variables for national origin ought to be equal to each other. In other words, if culture does not matter, national origin ought not to affect savings rates ceteris paribus. This is a null hypothesis involving 16 parameters and 16 equal signs:
![]()
The alternative hypothesis simply negates the null hypothesis, meaning that immigrants from at least one country have different savings rates than immigrants from other countries:
![]()
Now, if the null hypothesis is true, then an alternative, simpler model describes the data generation process:
![]()
Relative to the original model, the one above is a restricted model. We can test the null hypothesis with a new test statistic, the F-statistic, which essentially measures the difference between the fit of the original and restricted models above. The test is known as an F-test. The F-statistic will not have a normal distribution. Under the often-made assumption that the error terms are normally distributed, when the null is true, the test statistic follows an F distribution, which accounts for the name of the statistic. We will need to learn about the F- and the related chi-square distributions in order to calculate the P-value for the F-test.
F-Test Basics
The F-distribution is named after Ronald A. Fisher, a leading statistician of the first half of the twentieth century. This chapter demonstrates that the F distribution is a ratio of two chi-square random variables and that, as the number of observations increases, the F-distribution comes to resemble the chi-square distribution. Karl Pearson popularized the chi-square distribution beginning in 1900.
The Whole Model F-Test (discussed in Section 17.2) is commonly used as a test of the overall significance of the included independent variables in a regression model. In fact, it is so often used that Excel’s LINEST function and most other statistical software report this statistic. We will show that there are many other F-tests that facilitate tests of a variety of competing models. The idea that there are competing models opens the door to a difficult question: How do we decide which model is the right one? One way to answer this question is with an F-test. At first glance, one might consider measures of fit such as R2 or the sum of squared residuals (SSR) as a guide. But these statistics have a serious weakness – as you include additional independent variables, the R2 and SSR are guaranteed (practically speaking) to improve. Thus, naive reliance on these measures of fit leads to kitchen sink regression – that is, we throw in as many variables as we can find (the proverbial kitchen sink) in an effort to optimize the fit.
The problem with kitchen sink regression is that, for a particular sample,
it will yield a higher R2 or lower SSR than a regression with fewer X variables,
but the true model may be the one with the smaller number of X variables.
This will be shown via a concrete example in Section 17.5.
The F-test provides a way to discriminate between alternative models. It recognizes
that there will be differences in measures of fit when one model is compared
with another, but it requires that the loss of fit be substantial enough to
reject the reduced model.
Organization
In general, the F-test can be used to test any restriction on the parameters in the equation. The idea of a restricted regression is fundamental to the logic of the F-test, and thus it is discussed in detail in the next section. Because the F-distribution is actually the ratio of two chi-square (?2) distributed random variables (divided by their respective degrees of freedom), Section 17.3 explains the chi-square distribution and points out that, when the errors are normally distributed, the sum of squared residuals is a random variable with a chi-square distribution. Section 17.4 demonstrates that the ratio of two chi-square distributed random variables is an F-distributed random variable. The remaining sections of this chapter put the F-statistic into practice. Section 17.5 does so in the context of Galileo’s model of acceleration, whereas Section 17.6 considers an example involving food stamps. We use the food stamp example to show that, when the restriction involves a single equals sign, one can rewrite the original model to make it possible to employ a t-test instead of an F-test. The t- and F-tests yield equivalent results in such cases. We apply the F-test to a real-world example in Section 17.7. Finally, Section 17.8 discusses multicollinearity and the distinction between confi- dence intervals for a single parameter and confidence regions for multiple parameters.
Notes
1 Their actual model is, not surprisingly, substantially
more complicated. Return to text.
2 There were 17 countries of origin in the study,
including 900 households selected at random from the United States. Only married
couples from the same country of origin were included in the sample. Other
restrictions were that the household head must have been older than 35 and
younger than 50 in 1980. Return to text.
Excel Workbooks
ChiSquareDist.xls
CorrelatedEstimates.xls
FDist.xls
FDistEarningsFn.xls
FDistFoodStamps.xls
FDistGalileo.xls
MyMonteCarlo.xls
NoInterceptBug.xls